Player contribution

 

Methodology:

The methodology is the same as in the first-order Markov chain analysis with a few notable exceptions.

Zones 1 to Zone 15 have been condensed to Zone 1 — Zone 3 as outlined in Figure 1 below. Reason being that implementing a second-order model contributes to a significant increase in transient states which would be computationally demanding.

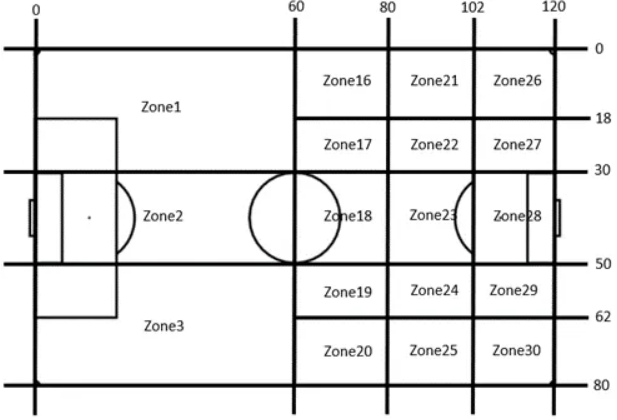
The two absorption states have been kept as Loss of possession and Shot. However, the transient state corresponds to the pairing of the current state with its preceding state. Having 18 zones combined with 4 set-piece states amounts to a total of 484 transient states to be considered. Table 1 presents possession 5, manipulated to suit a second-order model.

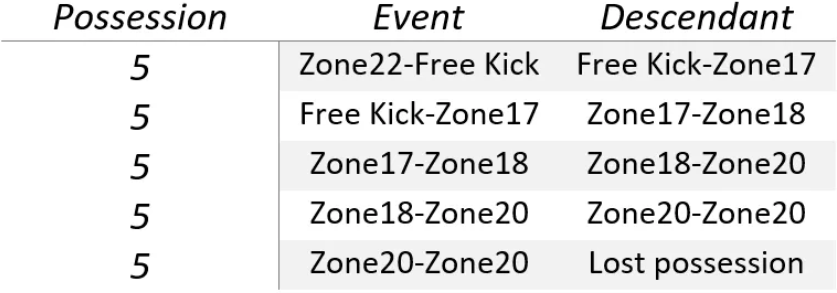
Constructing the matrices proved to be not as straightforward as in the first-order model. Having a second-order model firstly increased the amount of possible scenarios more than tenfold. Secondly, it resulted in some highly unlikely combinations for example:

Zone 1 — Zone 30 -> Zone 30 — Zone 1

Zone 1 — Corner -> Corner — Zone 3 etc.

This would result in many zero-sum columns in the matrices which is problematic. Excluding those whilst maintaining a square matrix would result in data loss. However, in the context of a football game, it is assumed that any events that have been linked to any of the pruned scenarios would have not had any significant contribution to shot generation. Therefore a decision has been made to prune the zero-sum cases which would reduce the transient states to 394.

Finally, the player contribution is calculated using the following formula:

Player contribution = Probability of a shot | Next event pair — Probability of a shot | Current event pair

Results:

Figure 3 presents the results from the second-order model compared to the first-order one.

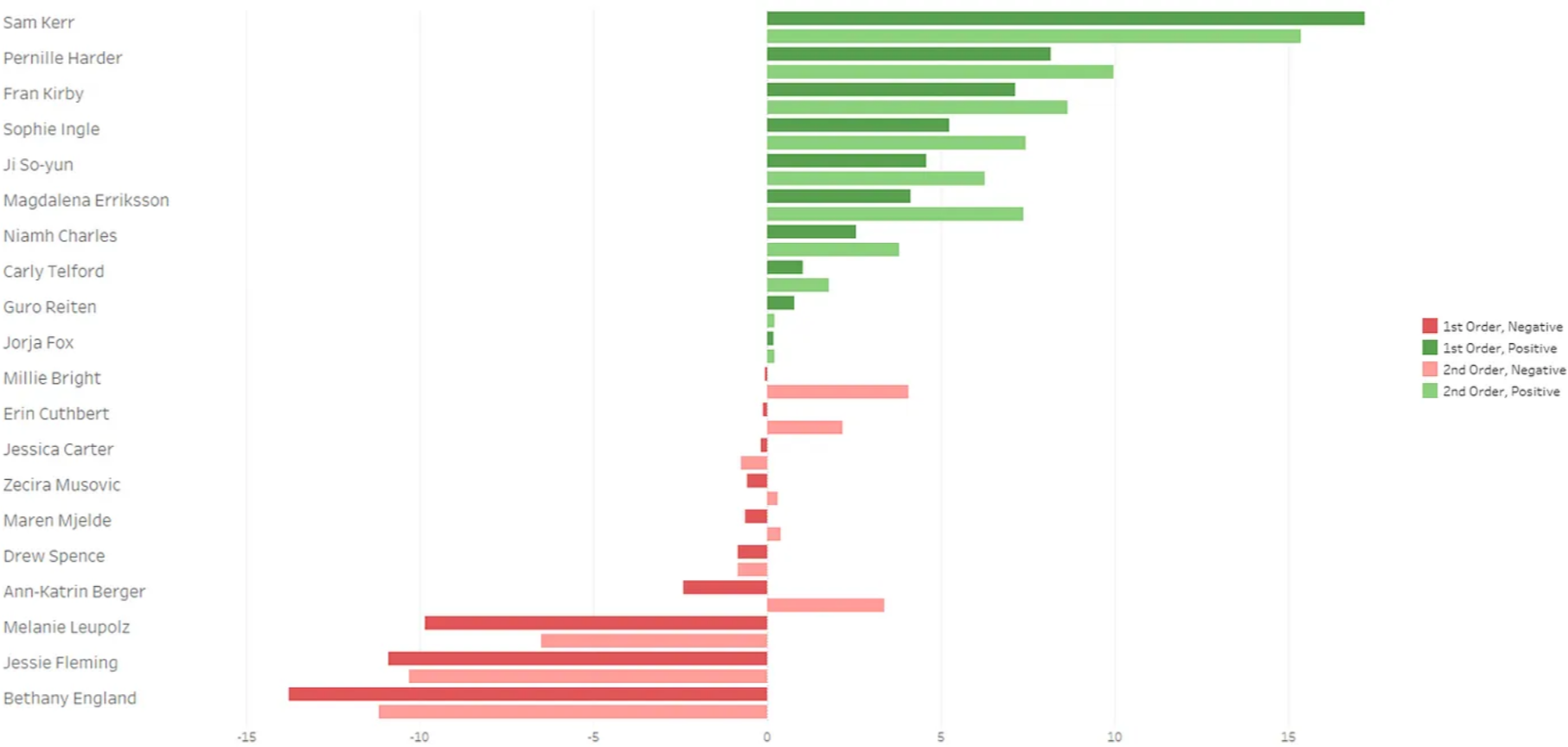
Looking at Figure 3 it can be concluded that applying a second-order Markov model does make a difference in the outcome for shot contribution. Most of the players have had a positive change in contribution with a notable exception being Sam Kerr. This implies that most players have been losing possession when there was little possibility to progress the attack, meaning that when they get an opportunity to create a shot they are converting more than the first-order model suggests. Another reason can be the fact that the zones have been reduced to 18 which lowers the shot possibility of zones closer to the halfway line as they are put in the same category as the least shot potent zones. Although absolute contribution has improved, when comparing players, the order has not changed dramatically, meaning that all players benefit from the second-order model in the same manner. Notable exceptions to that are Ann-Katrin Berger and Millie Bright who seem to have benefited the most from the model.

Conclusion:

Implementing a second-order Markov model suggests that including the preceding event in the context of the current event makes a difference in the probability of creating a shooting opportunity. That is to the surprise of any person who has watched a game of football. However, it was interesting to see how certain players have benefited more than others, suggesting a certain play style. Insights can be derived from comparing the two models alone since it has proven that it highlights players who are frequently on the receiving end of an unfavourable event, whether it is a pass, a clearance or a dribble. Analysing all 30 zones would provide an even more accurate estimate of the above, however, such a process is computationally demanding and could not be performed.

Football sometimes is a cruel game. Watching a certain player who has not had an impact may suggest that he has had little contribution and most conventional statistics can back that claim, where in reality there was little opportunity to contribute in the first place. Models like this highlight such cases. The context can then be further examined and tactical considerations can be put in place in order to improve performance. Something which in the long run can make a difference.

Useful links:

Github: Evaluating player contribution - 2nd order
Medium: Evaluating player contribution - 2nd order